|
Dagens Philosoph : Eratosthenes |
11:44:14 |
 Eratosthenes
Eratosthenes' si er en algoritme til bestemmelse af primtal. For at bestemme alle primtal mindre end eller lig med feks. 100 opskrives alle de naturlige tal (større end 1) dvs. 2,3,...,100. Først overstreges alle lige tal (på nær 2), dernæst alle multipla af 3 (på nær 3).Der sættes løbende en ring om de tal der er afprøvede og godkendt som primtal. Man går derefter videre til næste tal uden ring eller overstregning. 
Eratosthenes' si med systematisk opstregning.
Bestemmelsen af Jordens størrelse
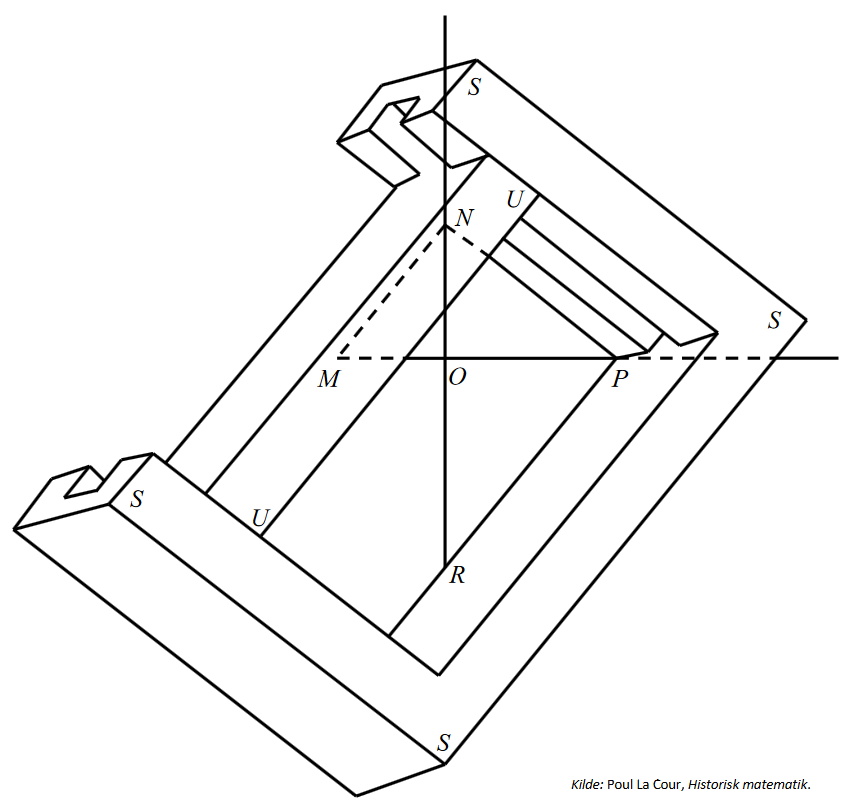
Eratosthenes måleopstillingTegningen herover er vist med overdrevne vinkler. Ill.: Møllers-Grafisk Tegnestue/Hans Møller. 
Kort over Ægypten, med Aleksandria og Aswan = det daværende Syene.
Der blev fundet en praktisk løsning, som f.eks. ovenstående, der efter overleveringen skulle være en skitse af det apparat, Eratosthenes Akademi konstruerede til løsning af det deliske problem. |
Eratosthenes fra Kyrene 276 f.Kr. - 194 f.Kr.
Indholdsfortegnelse :Om EratosthenesEratosthenes' si Som algoritme for computerkode Fordobling af en ternings volume Eratosthenes mekaniske løsning Moderne metode Fordobling af terning: Flerdobling af terning: Måling og beregning af Jordens omkreds
Om Eratosthenes 🔝Eratosthenes (født 276 f.Kr., død 194 f.Kr.) var en græsk astronom og matematiker, som bestemte Jordens omkreds ved måling af Solens højde i henholdsvis Alexandria og Syene (det nuværende Aswan) på samme tidspunkt. De 2 byer ligger på (næsten) samme længdegrad, men med en nord - syd afstand på 900 km. imellem sig. Derudfra kunne han beregne jordens krumning og dermed også omkredsen.Eratosthenes resultat, at Jorden er kugleformet, blev ikke kendt eller accepteret i det katolske Europa i Middelalderen. Han var leder af Biblioteket i Alexandria og han fandt en metode til at fastlægge primtallene, kaldet Eratosthenes' si. Eratosthenes var en af oldtidens mest alsidige forskere inden for sprog, historisk kronologi, litteratur og især naturvidenskab. Han var leder af biblioteket i Alexandria. Eratosthenes beskrev en mekanisk løsning af problemet om terningens fordobling, kaldet det deliske problem, og en teoretisk metode til at finde primtal, kaldet Eratosthenes' si. Eratosthenes' si 🔝Eratosthenes' si er en talrække, der fås ved at markere nogle tal (her mærket med understregning). At ryste sien betyder at man mærker det mindste af de hidtil umærkede tal, og lader alle egentlige multipla af dette tal drysse ud af sien. Rækken startes ved at man fylder sien op med tallene større end 1; alle umærkede, dvs.
Primtallene op til 101 er flg. 26 tal:
Ingen tal går op i et primtal (pånær 1 og sig-selv) og det er det "Eratosthenes' si" lukrerer på ved at luge al redundans bort. En anden måde at luge ud i talmængden af potentielle primtal (der er større end 7) er at betragte mønsteret af allerede fundne primtal og dér fokusere på det sidste ciffer. I blandt disse findes ingen lige primtal (større end 2) og der findes ingen primtal (større end 5) der ender på 5. Tilbage er kun cifrene: 1, 3, 7 og 9. Herved udelukkes de første 60% af samtlige mulige kandidater til primtal. Der er dog stadig mange IKKE-primtal i de sidste 40% af kandidaterne. Primtal under 1.000.000 udgør feks. kun ca. 7,85% af talmængden. Leg selv med primtal her: Link. Som algoritme for computerkode 🔝For matematisk computerprogrammering til beregning af primtal er Eratosthenes' si den hurtigste algoritme at bruge som basis for programmets kode, uanset programsprog. Det skyldes at algoritmen ikke anvender division. I computerens CPU koster addition, subtraktion og multiplikation af heltal kun to cykler at udføre, mens division kræver mindst 17 cykler, ofte endnu flere. Der findes derudover mange måder at optimere koden på, især hvis man søger efter verdensrekorden for største primtal. (Men al form for division må begrænses, inkl. modulus).Fordobling af en ternings volume 🔝Fordobling af en ternings volume er et længe kendt problem, som også Eratosthenes grublede over. Selve løsningen ved brug af kun passer og lineal var ikke mulig i oldtiden og er det stadig ikke. De kendte ikke til brugen af "skæve" værdier ift. kvadratrødder og kubikrødder mfl., som feks. kvadroden af 2 eller kubikroden af 2, der jo er kendt for aldrig at kunne "gå op". Kvadratroden af 4 og kubikroden af 8 er nemme at indse ved hovedregning, men 2, 3 og 5 mv. er problematiske.Dermed var grunden lagt til et af de mest langlivede studier, De tre "uløselige" problemer: cirklens kvadratur, terningens fordobling (deliske problem) og vinklens tredeling, som netop ikke kan løses udelukkende med passer og lineal. Eratosthenes mekaniske løsning 🔝Eratosthenes beskrev en mekanisk løsning af problemet om terningens fordobling, kaldet det deliske problem.Det skulle vise sig, at det ikke var muligt at løse det deliske problem, alene med brug af passer og lineal. Men arbejdet var dog langt fra spildt. Der kom en række praktiske løsninger ud af det, som f.eks. det der er vist skitsen til venstre, som efter overleveringen skulle forestille det apparat, Akademiet konstruerede til løsning af det deliske problem. Moderne metode 🔝Nu om dage med regnemaskiner, feks. en alm. lommeregner eller mobiltlf. mv. er sagen en ganske anden ift fordobling af en terning.Formlen:
Hvor V2=Den dobbelte ternings volume, S=sidelængden af den oprindelige terning, Cbrt(2)=kubikroden af 2 (= den tredie rod af 2). Giver den fordoblede ternings volume hvor den nye sidelængde er:
Fordobling af terning: 🔝Så hvis man fordobler terningen med siden: S1=1, bliver S2 = ca. 1,2599210498948731647672106072782Flerdobling af terning: 🔝Vil man 3 (eller flere) doble terningen så brug følgende, formel:
En 8 dobling af terning med sidelængde: 1, giver sidelængden: 2,0: lige præcis, sjovt nok. Måling og beregning af Jordens omkreds 🔝Eratosthenes viste ved observation og beregning, at Jordens omkreds er ca. 45.000 km (i dag målt til 40.092 km). Han observerede, at ved sommersolhverv kaster viseren i soluret i Syene (Aswan) ingen skygge, mens soluret i Alexandria kaster en skygge på a=1/50 af urets omkreds. Da solurene er ligedannede med jordkloden, er vinkelforskellen mellem de to byer en-halvtresinds-tyvende-del (1/50) af Jordens omkreds, som derfor bliver 50 gange afstanden på 900 km. mellem byerne, altså ialt ca. 45.000 km.Tegningen (til venstre) er vist med overdrevne vinkler. Han målte Solens zenitafstand ved sommersolhverv i Alexandria til præcis en-halvtresinds-tyvende-del (1/50) af meridianen og beregnede derved Jordens omkreds til 250.000 stadier; hans geografiske arbejder var grundlæggende for eftertidens forståelse af Jorden som en kugle, og hans stjernekort fastlagde stjernebilledernes navne og udseende. Han levede som samtidig med Aristarchos af Samos, der også fandt frem til, at Jorden ikke er flad men en globe. Eratosthenes var ven med Archimedes, som anerkendende dedikerede ham sit værk Metoden. Archimedes var ham med badekarret: "Hvis man nedsænker et legeme i vand, så ...", nej - det har ikke noget med telefonen at gøre. Archimedes' lov siger nemlig, at når et legeme helt eller delvis nedsænkes i en væske, taber det lige så meget i vægt, som den fortrængte væskemængde vejer. Man kan da sige, at legemet foruden tyngden (gravitationskraften) er påvirket af en opadrettet kraft, opdriften. |
|
