|
Dagens Philosoph : Pythagoras |
11:47:07 |
 Bust of Pythagoras. Roman copy of Greek original. Capitoline Museums, Rome.
I dette udsnit af Rafaels freske sidder Pythagoras i skægget profil. Bag ham ses Hypatia af Alexandria i en hvid kjole..jpg)
Pythagoras blev begravet ved dette tempel: Hera Temple, Metaponto, Provincia di Matera, Basilicata, Italy
Udregning af hypotenusens længde i plan-geometrien.
Udregning af diagonalens længde i rum-geometrien.
Illustration af den pythagoræiske læresætning
Animation af et dodekaeder.
La Grande Arche | Den nye Triumfbue i fire dimensioner i Paris, Frankrig. Den nye triumfbue i Paris har danske aner, for monumentet er tegnet af Johan Otto von Spreckelsen. Den danske arkitekt vandt i 1982 en international konkurrence udskrevet af den franske præsident, og han kunne tre år senere opleve realiseringen af sin idé om en moderne triumfbue til ære for menneskeheden og humanistiske idealer. 
Irrationale tal er i matematikken alle tal der er reelle, men ikke rationale.De klassiske eksempler er tallet π = 3,1415926... (cirka) Kvadratroden af to som skrives √2 er et irrationalt tal. Kvadratrod to er lig med 1,414213562373095... (cirka) |
Pythagoras fra Samos, 570 f.Kr., - 495 f.Kr.
Indholdsfortegnelse :LivLære Tallenes magi Læresætningen a² + b² = c² Udvidet brug af Pythagoras sætning a² + b² + c² = d² a² + b² + c² + d² = e² Eksempel på fjerde dimension Og hvad kan man så bruge det til ? Opdagelsen af irrationale tal
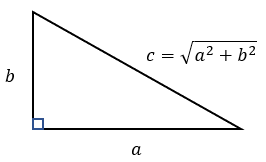
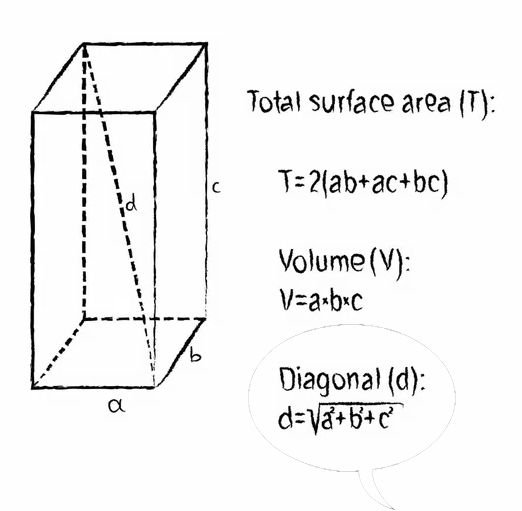
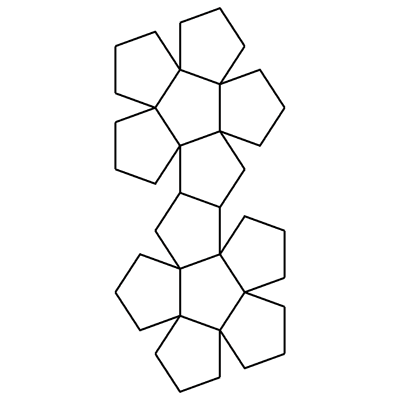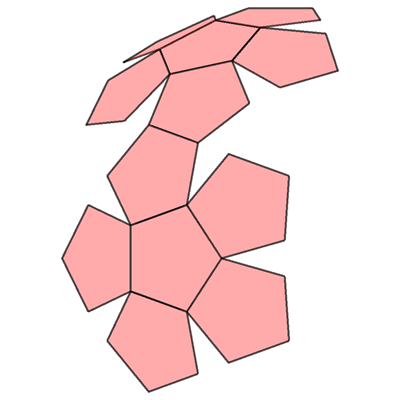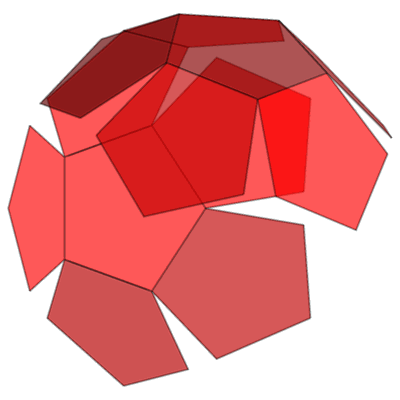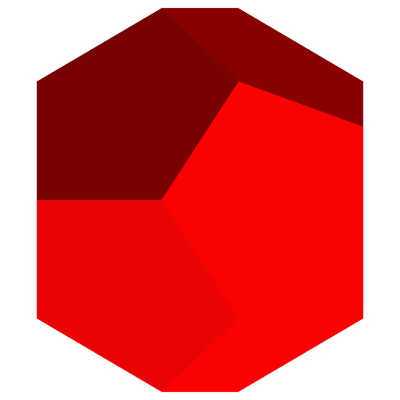
Pythagoras fra Samos (født 570 f.Kr., død 495 f.Kr.) var en græsk filosof, mystiker, matematiker, musikteoretiker og musikterapeut. Liv 🔝Forældrene: faderen Mnesarkhos, der var sølvsmed og moderen Pythaïs, der var efterkommer af Ancaeus, Samos grundlægger. Pythagoras var elev af Thales og dennes elev Anaximander fra Milet, der havde opfundet et enkelt solur og foregreb Darwins tanker om menneskenes oprindelse og Pherekydes fra Syros, mystikeren, der troede på sjælevandring. I sin ungdom rejste Pythagoras vidt omkring, hvorefter han vendte han hjem til Samos, hvor tyrannen Polykrates skal have benyttet ham til diplomatiske opgaver. Omkring 530 f.Kr var Pythagoras imidlertid etableret i den græske koloni Kroton i Syditalien, hvor han grundlagde et religiøst fællesskab. Disse pythagoræere var ressourcestærke personer, der snart stod for koloniens styre; efterhånden fik de betydelig magt også indenfor Magna Graecia. Det skabte en storm af modvilje mod dem, og rygter om, at de bedrev trolddom. Mod slutningen af sit liv blev Pythagoras udvist fra Kroton til Metapontion; hans tilhængere blev ligeledes sendt i eksil eller dræbt og deres forsamlingshuse nedbrændt.Pythagoras skal have giftet sig med en af sine elever, Theano. Oplysningerne om hende er meget modstridende. Breve og fragmenter, der sagdes at være fra hendes hånd, kan være forfalskninger. Theano var et ret almindeligt navn, blandt andet hedder Athenes præstinde i Troja Theano hos Homer; ligesom en af danaiderne hedder Theano. Der kan altså godt have været flere pythagoræere med det samme navn, som så er blevet forvekslet. Der er også modstridende oplysninger om børnene, hun fik med Pythagoras. De fik datteren Damo og sønnen Telauges; takket være Damo blev noget af indholdet i Pythagoras' lære bevaret. Andre opgiver fem børn, pigerne Damo, Arignote og Myia og brødrene Telauges og Mnesarkhos. Theano og hendes døtre skal have været læger. Efter pythagoræernes opfatning var menneskekroppen en miniature af universet. I en diskussion med lægen Euryphon om fosterets udvikling, skal Theano og døtrene have argumenteret for, at et menneskefoster er levedygtigt efter syvende måned. Lære 🔝I løbet af 600-tallet f.Kr. voksede noget frem hos grækerne, som man ikke så hos noget andet folkeslag. De lærte af egypternes beregninger; men hvor egypternes matematik altid havde en praktisk hensigt, enten det gjaldt at få pyramiderne rejst eller at overvåge Nilens oversvømmelser, var det først hos grækerne, at matematik blev dyrket for sin egen skyld, som en rent teoretisk videnskab. Det samme gjaldt astronomien, som de lærte af babylonierne, hvis observationer tjente et rent praktisk formål, nemlig astrologien knyttet til deres religionsudøvelse. Her var det astronomien, grækerne gjorde til en teoretisk disciplin; og ordet "teori" kommmer da også af græsk theoria i betydningen "hellig/guddommelig beskuen" (theós = Gud), dvs. en måde at betragte verden på, der er løsrevet fra vore hverdagslige projekter. Det drejer sig om en beskuelse og deraf følgende indsigt, kun for denne indsigts egen skyld.Alt i universet blev nu anset som noget, det var muligt for mennesket at kunne nærme sig med sin tanke. Det er fra pythagoræerne, vi har fået ordet "matematik", af græsk mathēmatikē téchnē (= læreteknik, kunsten at lære). En af deres indsigter var, at alt i virkeligheden kan tilbageføres til tal, samt forhold tallene imellem. Det interessante ved Pythagoras' bevægelse er, at man ikke kun skulle frigøre sjælen ved hjælp af askese, men også anså filosofiske tanker og videnskabelige studier som en måde at rense sjælen på, parallelt med et fokus på det fysiske helbred. Mange af antikkens læger var pythagoræere. Pythagoras skal have været den første til at indføre begrebet "filosofi" som et ord for at beskrive kærlighed til og interesse for visdom, der hjælper sjælen til at finde sig til rette i kosmos. Men da han hørte sig omtalt som en af Grækenlands "syv vise mænd" (sofister), skal han have sagt, at han ikke var nogen sofist/vismand, men en filosof - en, der elskede visdom. Ligesom Sokrates blev undervist i filosofi af en kvinde, Diotima, blev det sagt, at Pythagoras lærte sine moralske doktriner af Themistoklea, der var præstinde ved oraklet i Delfi. Pythagoræerne lagde vægt på ægteskabelig troskab for både mænd og kvinder. Deres fællesskab var revolutionerende for sin tid, da det tillod kvinder at være medlemmer. I Iamblichus' liste over pythagoræere findes 218 mandsnavne og 17 kvindenavne. Der er ikke overleveret skrifter fra nogen af disse kvinder, selv om der i senere tid blev præsenteret forfalskninger. Pythagoras selv har heller ikke efterladt sig skrifter, og der findes heller ingen detaljerede overleveringer fra hans samtidige, da hans tilhængere måtte sværge tavshed ved optagelsen og aldrig røbe de indsigter, fællesskabet gav dem del i. I de sidste århundreder f.Kr. kom det på mode at præsentere ham ret uhistorisk som en halvguddommelig skikkelse, der var ophav til alt, der var rigtig i græsk filosofi, deriblandt mange af Aristoteles' og Platons tanker. En række skrifter blev forfalsket for at underbygge dette. Ifølge Aristoteles troede folk i Kroton, at Pythagoras var søn af Apollon, og det blev sagt, at "der er guder og mennesker og skabninger som Pythagoras". Iamblichus fortæller, at da pythagoræerne Myllias og hans gravide kone Timycha blev taget til fange af tyrannen Dionysius, blev Myllias spurgt, hvorfor hans fæller hellere ville dø end træde på bønner. Myllias svarede, at han selv hellere ville træde på bønnerne, end forklare Dionysius noget om sagen. Tyrannen lod Myllias føre bort; og Timycha, der blev holdt tilbage, bed angiveligt sin tunge af, så hun ikke under tortur kom til at røbe bevægelsens hemmeligheder. Tallenes magi 🔝Ifølge en legende gik Pythagoras en gang forbi en smedje, da det slog ham, at lyden fra en tung hammer er dybere end lyden fra en lettere. og da han vidste, at to lette lod kan opveje et tungere, stod det klart for ham, at toneintervaller i musikken også kan opfattes som et forhold mellem tal. På et strengeinstrument afgøres tonens højde af strengens længde. For Pythagoras var dette bevis for, at alt i virkeligheden består af tal. Naturfilosofferne i Milet søgte efter "urstoffet", der udgør virkelighedens tilgrundliggende princip; nu kom Pythagoras frem til, at virkelighedens inderste princip i stedet er tal. Hans forhold til tal tog dermed udgangspunkt i det anskuelige. For at markere antal, benyttedes småsten lagt i mønstre. Og da en lille kalksten på latin hedder calculus, fik man ordet "kalkulering".Pythagoras forenede i sin lære matematik og talmystik med musik (både udøvelse og teori) og forestillingen om sjælens udødelighed. Han skal have fortalt sine tilhængere, at han en gang havde været Aethalides, søn af Hermes, som indrømmede ham et ønske - dog ikke udødelighed. Pythagoras bad om at måtte huske alt, hvad der skete ham, både levende og død. En af de inkarnationer, han skal have påstået at huske, var som Euphorbos, der blev dræbt af Menelaos i Iliaden. Derefter blev han Hermotimos, som i Apollons tempel genkendte Menelaos' skjold (viet til Apollon på hjemrejsen fra Troja). Hans næste inkarnation var som fiskeren Pyrrhos fra Delos, og så Pythagoras. Læresætningen 🔝Pythagoras har lagt navn til den pythagoræiske læresætning om forholdet mellem længden af siderne i en retvinklet trekant. Princippet var velkendt både for egyptere og babyloniere længe før Pythagoras' tid, når det gjaldt en trekant med målene 3, 4 og 5; men Pythagoras beviste, at princippet gjaldt i alle tilfælde.Det lyder: Summen af kateternes kvadrater, i en retvinklet trekant, er lig med kvadratet på hypotenusen. I symbolsk notation: a² + b² = c² 🔝Se også illustrationen til venstre.Udvidet brug af Pythagoras sætning 🔝Det giver lidt sig selv, at man også kan bruge bruge Pythagoras sætning til at beregne diagonaler i hhv. kvadrater og rektangler, da disse figurer jo består af sammensatte, retvinklede, trekanter med hypotenuserne som diagonal.Men hvad med en terning eller en retvinklet kasse? Kan man beregne afstanden mellem 2 modstående hjørner (den indre rumlige afstand) vha. Pythagoras? Svaret ligger ligefor - JA selvfølgelig kan man det. Man sætter blot et led mere på formlen (Se også illustrationen til venstre) : a² + b² + c² = d² 🔝Sådan ! - Men vidste Pythagoras og hans ligestillede, at det var så enkelt ?Nu kommer vi så til noget der er tricky! Vi sætter yderligere et led på formlen og går således fra 3 dimensioner til 4 dimensioner : a² + b² + c² + d² = e² 🔝Og hvor er vi så nu? Kun de færreste kan forestille sig den 4. dimension. Hvilken retning peger den imod? Er det måske "tiden" vi har fat i? Jeg har ikke svaret, måske har Spreckelsen (Se også billedet til venstre), men jeg tror ikke vi skal spørge Pythagoras. Fakta er dog at Pythagoras formel også gælder i den 4. dimension. Imponerende !Fakta: 5, 6, 7, ... Formlen bliver ved med at fungere i stigende dimensioner, ingen ved hvor langt, men det er ikke matematikken der sætter grænsen ! Eksempel på fjerde dimension 🔝I fysikken er rumtid defineret som en matematisk model, som kombinerer vores tredimensionale syn på universet med tid. Rumtid er sædvanligvis tolket som firedimensionale objekter hvor objektet har de tre kendte rumdimensioner, i tillæg til tid som en fjerde dimension.Rumtid Begrebet rumtid er i nyere tid blevet en fællesbetegnelse på teorier som går udover de tre dimensioner. Hvor mange dimensioner man faktisk må tage i brug for at beskrive universet, er stadig et åbent spørgsmål. Strengteorien tilsiger, at vi har fra 10 til 26 dimensioner !!! I Albert Einsteins specielle og generelle relativitetsteori er tid og det tredimensionelle rum slået sammen til en enkel firedimensionel mangfoldighed kaldet rumtid. Et punkt i rumtiden bliver benævnt en hændelse. Enhver hændelse har fire koordinater: (t, x, y, z). Dette fænomen kan ses som en masse 3 dimensionelle plader, der er stablet, hvilket giver det fulde billede af en ellers tidsmæssig handling. Og hvad kan man så bruge det til ? 🔝Jo forestil dig en flue i en ellers tom jernbanevogn der kører afsted med en vældig, men dog kendt, hastighed. Hvis fluen nu starter i det ene hjørne af vognen og så flyver (med en kendt hastighed) til det modstående hjørne, hvor langt har fluen så flyttet sig i forhold til omgivelserne uden for vognen ?Og hvor langt i forhold til solen eller universets centrum ? Mentalplanet LIVET PÃ MENTALPLANET Rummet på mentalplanet er 5-dimensionalt. Det betyder, at man ikke alene ser alt fra én vinkel som i den 3-dimensionale verden plus den 4. dimension i den astrale verden, hvor man ser rundt om genstanden i én samlet oplevelse. Nu oplever man, at man samtidig er inde i genstanden, på trods af at man ser den udefra. Man ser genstanden udefra, omkring den og indefra. Denne beskrivelse gælder naturligvis ikke kun genstande på mentalplanet. Det gælder alt i denne region. Det medfører, at alt er til stede i bevidstheden på én gang. Man er derfor ét med alt. Det er umuligt at forestille sig med en tredimensional fysisk hjerne. Opdagelsen af irrationale tal 🔝Pythagoræerne var splittet i to grupper, acusmatici, der modtog Pythagoras' mundtlige instruktioner om, hvordan man skal leve (acusmata = "noget, man har hørt"), mens mathêmatici hævdede, at Pythagoras ved sin ankomst til Italien aldrig rigtig fik anledning til at sætte øvrighedens ledende mænd ind i, hvad hans videnskab gik ud på, så det i stedet var mathêmatici, der forvaltede hans videnskab. Hippasos fra Metapontum huskes for historien om, at broderskabet skulle have druknet ham, fordi han havde grublet over kvadratroden af 2, og kommet frem til det, pythagoræerne kaldte et irrationalt tal.Note: Irrationale tal er i matematikken alle tal der er reelle, men ikke rationale. I vore dage er de ikke usædvanlige. Se desuden skitsen t.v. Nogle af de klassiske eksempler er tallet π = 3,1415926... (cirka) Kvadratroden af to som skrives √2 er også et irrationalt tal. Kvadratrod to er lig med 1,414213562373095... (cirka) Det er Plutarch, som først omtaler en skandale, fordi nogen havde røbet eksistensen af irrationale tal; men Plutarch skriver ikke noget om, at nogen blev straffet for at have røbet fundet. I Pappus af Alexandrias senere version forlyder det imidlertid, at den, der røbede eksistensen af irrationale tal, var blevet druknet som straf. Iamblichus gengiver to versioner: I den ene udvises den skyldige, og en gravsten blev rejst for ham, for rigtig at understrege alvoret; i den anden version druknes personen, men for at have fremvist et diagram af et dodekaeder, en figur sammensat af tolv femsidede flader (Se illust. i venstre spalte). Moderne forskere har foreslået, at Hippasos kan have opdaget irrationale tal gennem sit arbejde med et dodekaeder; men ingen antik kilde knytter Hippasos eller dodekaeder til opdagelsen af irrationale tal. Historien om, at Hippasos blev druknet som straf for at have fremvist i offentlighed, et diagram af et dodekaeder passer ikke med udviklingen i græsk matematik, hvor det var Theaetetus, der senere i 300-tallet f.Kr., var den første, der studerede den mangesidede figur. At fremvise en tolvsidet figur i offentlighed kunne heller ikke skandalisere nogen. Den mest sandsynlige forklaring er, at et dodekaeder tjente som kultgenstand for pythagoræerne; sådanne figurer er fundet fra forhistorisk tid, udført i sten og bronze. Det kan være Hippasos' arbejde med en hellig genstand, der var årsag til forargelsen. |
|
