
|
Dagens Science : Insekter |
18:08:52 |
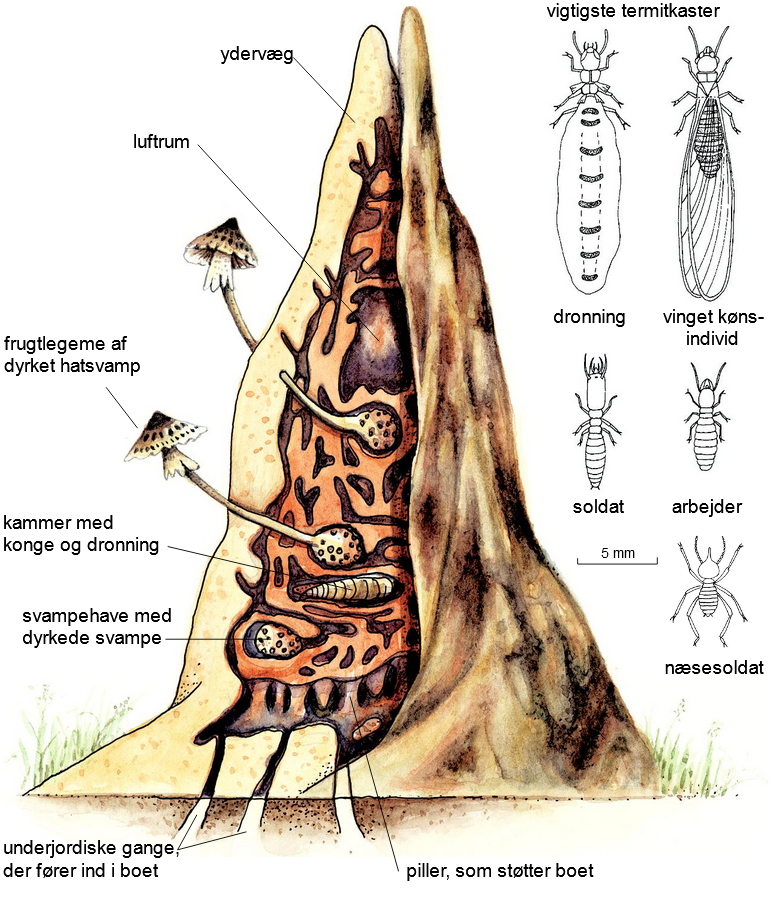
Centralt i det 2-3 m. høje bo findes kongens og dronningens kammer. 


Myrelarverne udskiller silke, som bruges til at hæfte boet sammen. 


Hele 60 procent af den voksne guldsmeds krop består af flyvemuskler.




Tofarvet frømøl er lysegrå på forreste tredjedel, mens den øvrige del er glinsende kobberrød. Larven er gulhvid med mørkebrunt hoved. Larven er 12-13 mm lang, når den er fuldt udviklet. Det voksne møl er knap en centimeter langt. 
Larven er 15-19 mm lang, mens et voksent melmøl er 20-22 mm. Altså noget større end Frømøllet. 
Denne metode til effektiv forebyggelse er fuldstændig fri for insektgifte. Den tiltrækker og fanger både melmøl og tofarvet frømøl, som er de mest almindelige mølarter i nordiske køkkener. Fælden kan anvendes året rundt og er helt lugtfri, hvilket gør den ubesværet at bruge uden at forstyrre omgivelserne. Hver fælde har en levetid på op til 6 uger. Der er integreret feromon for at maksimere effektiviteten. 


De fleste møl har en livscyklus, som kan opdeles i 4 etaper. Gælder husmøl (dvs. klædemøl, pelsmøl, frømøl og tofarvede møl) – ikke de øvrige 160.000 mølarter!


Menneskeloppen (Pulex irritans) er en type lopper, der findes på mennesker. Den er sjælden i Danmark, men almindelig i Sydeuropa.
A: Hoved B: Bryststykke C: Bagkrop 1. følehorn 2. punktøjne (nedre) 3. punktøjne (øvre) 4. facetøje 5. hjerne (cerebral ganglion) 6. forbryst (prothorax) 7. dorsalt blodkar 8. trachérør og spirakle (trachéens åbning i kutikulaen) Åndedrætsorgan 9. midtbryst (mesothorax) 10. bagbryst (metathorax) 11. forvinge 12. bagvinge 13. midttarm eller mave 14. hjerte 15. ovarium 16. bagerste mave (tarm, rectum & anus) 17. anus 18. æggestok (oviduct) og sædgemme 19. bugnernesnor (abdominal gangliekæde) 20. malpighiske rør 21. trædepude 22. klo 23. fod eller fodled (tarsus) 24. ben (tibia) 25. lår (femur) 26. hoftering (trochanter) 27. fortarm (kro) 28. nerveknude (ganglion) 29. hofte (coxa) 30. spytkirtel 31. baghjerne eller det forreste ganglion (ganglion suboesophagicum) 32. munddele; fra venstre: overlæbe (labrum), overkæbe eller kindbakke (mandibel), underkæbe (maxil) med antennelignende palpe, underlæbe (labium) med palpe
|
Videnskab om: Bier, myrer termitter
Indholdsfortegnelse :Hvad er sociale insekterInsektkolonier fungerer som individer Kolonierne følger reglerne Vævermyrer bruger larver som limpistol Termitter bruger afføring som medicin Bakterier holder kolonien i live Hveps har solcelleanlæg indbygget i skjoldet LUFTAKROBATIK guldsmede Husfluen Hvor hurtigt flyver en spyflue Hvorfor kan man ikke klaske en flue med hånden, men godt med fluesmækkeren Fluer på PC skærmen Frømøllet - Køkkenmøllet Frømøl, myslimøl Frømøllets historie Er der brunlige insekter i dit hjem Møllets liv og udvikling Livscyklussens trin Møl er ikke farlige eller giftige! Sådan undgår du møl i madvarerne Økologi, giftfri madvarer vs. frømøl Melmøl, hold dit hjem frit for dem Sådan forebygger du angreb fra melmøl Hvis skaden er sket Elektriske Mølfælder Cedertræ imod møl Skægkræ Sølvkræ - Sølvfisk Ildtæge - Kastaniemøl Ildtæge Kastaniemøl Insekters indre anatomi Tarmkanalen Nervesystemet Reproduktion Insekters respiration og cirkulationssystem
Hvad er sociale insekter 🔝Sociale insekter er karakteristiske ved at have opbygget samfund med dronninger, der fortrinsvist lægger æg og arbejdere, der er ufrugtbare, men tager sig af afkom og bo.Tidligere studier (primært hos honningbien) har vist, at dronningen udskiller et specifikt duftstof, der holder styr på arbejderne og bevarer dem ufrugtbare. Disse duftstoffer fortæller os en masse om, hvordan sociale insekter har udviklet sig, og hvordan deres sociale adfærd er styret og kontrolleret. Dronninger benytter duftstoffer til at signalere, hvilken umiddelbar tilstand boet er i. Blandt andet kan hun udskille feromoner, der fortæller arbejderne, at hun lægger mange æg, og hun derfor er en effektiv mor, der gør, hvad hun er bedst til. Danske forskere har opdaget, at arbejdermyrer selv kan udvikle æggestokke og begynde at lægge æg, hvis de ikke kan lugte, at dronningen er i nærheden. Feromoner hos andre sociale insekter, herunder hvepse og termitter, er endnu ikke påvist i samme grad. Forhåbentlig vil forskning i fremtiden være med til at vise, hvorvidt feromoner er en universel kommunikationsform hos sociale insekter. Og måske kan feromonerne lære os, hvad de enkelte typer feromoner fortæller. Med andre ord: Hvad der bliver sagt på ‘insekt-sprog'. Insektkolonier fungerer som individer 🔝En række af de biologiske regelmæssigheder, der gælder for enkelte dyr, gælder også for hele kolonier af insekter. Det understøtter ideen om at betragte insektkolonier som superorganismer.Insektkolonier som dem, man finder i en myretue eller i et bistade, er imponerende samfund, hvor en masse individer arbejder mod samme mål. Insekterne specialiserer sig og kan i fællesskab udrette utrolige ting. For eksempel kan en million termitter bygge et otte meter højt termitbo med et effektivt ventilationssystem. De enkelte insekter har ikke de store evner udi arkitekturens svære kunst, men tilsammen klarer de sig fantastisk. Det har fået visse forskere til at kalde insektkolonier for superorganismer. På samme måde, som cellerne i vores krop er specialiserede og ‘arbejder sammen' om at holde liv i os og måske endda føre slægten videre, kan de enkelte insekter forstås som dele af én stor superorganisme. Spørgsmålet er, hvor langt analogien rækker – i hvor høj grad, man kan sammenligne insektkolonier med individer, der lever alene. Nu har en gruppe forskere leveret en del af svaret: Ganske langt, viser det sig! Kolonierne følger reglerne 🔝De amerikanske biologer har analyseret data om 168 forskellige insektsamfund blandt myrer, termitter, bier og hvepse. Og de kunne vise, at man rent matematisk godt kan forsvare at kalde kolonierne for superorganismer – forstået på den måde, at kolonierne følger de samme biologiske regler som enkelte individer.Forskerne undersøgte blandt andet, om koloniernes stofskifte er proportional med insekternes samlede masse opløftet i trekvart potens. Sådan er det nemlig generelt med dyr. En kat er cirka 100 gange tungere end en mus, men dens stofskifte er ikke 100 gange større – i stedet er stofskiftet nærmere 100 opløftet i 3/4 = 31,6 gange større. Den sammenhæng, som kaldes Kleibers lov, kan man genfinde hos rigtig mange levende organismer, fra bakterier til blåhvaler. Og nu har forskerne altså vist, at den også gælder for insektkolonier – i hvert fald næsten, for potensen blev målt til 0,81 i stedet for 0,75. Vævermyrer bruger larver som limpistol 🔝De fleste myrer holder sig på jorden, men vævermyrerne foretrækker en penthouselejlighed. Myreboet er på størrelse med en badebold og dingler ned fra trætoppene.Arbejdermyrerne, som står for byggeriet, er blot fem-ti mm lange, hvilket ikke er meget, når myrerne skal trække store blade sammen inden selve vævningen. Udfordringen klarer myrerne i et tæt samarbejde – de hægter sig sammen i kæder med den enes kæbe om den andens talje. På den måde kan hundredvis af myrer skabe et mere end 20 cm langt tov, som giver adgang til bladene. Herefter klistres løvet sammen ved hjælp af limpistoler – myrernes egne larver, som i modsætning til de voksne spinder silke. Med kæberne holder arbejdermyren fast i en larve og fører den frem og tilbage mellem bladkanterne, så de føjes sammen. Termitter bruger afføring som medicin 🔝Frisk termitafføring har et stort indhold af bakterier og mikroorganismer. De lever i symbiose med termitterne i deres tarmsystem og gør det muligt for insekterne at fordøje træ.Men ekskrementerne er også den rene lækkerbisken for bakterier af slægten Streptomyces, som producerer en række stoffer, der dræber sygdomsfremkaldende organismer, bakterier, virus eller svampe. Termitterne bor med andre ord i en fæstning af medicin af egen produktion. Og medicinen er imponerende effektiv. Bakterier holder kolonien i live 🔝Termitters overlevelseschancer afhænger af, hvilke mikroorganismer der findes i deres bo. Når boet er fyldt med Streptomyces-bakterier (orange), som bekæmper svampe og andre bakterier, overlever ca. 85 pct. af termitterne i en periode på 60 dage.Bakterien giver endda bedre overlevelseschancer end i et sterilt kontrolmiljø (blå). Men hvis Streptomyces fjernes, og en svamp i stedet tilsættes, overlever kun cirka halvdelen af kolonien. Ikke alene er termitter sjældent syge – de er også godt beskyttede mod mange moderne bekæmpelsesmidler, der, i et forsøg på at undgå pesticider, er baseret på brugen af netop mikroorganismer. Termitternes hjemmedyrkede medicin er så effektiv, at medicinalfirmaer nu forsker intenst i at udvinde den. Håbet er at kunne udvinde nye former for antibiotika til bekæmpelse af bl.a. multiresistente bakterier. Hveps har solcelleanlæg indbygget i skjoldet 🔝Forskerne har hidtil troet, at planter og enkelte bakterier var de eneste, som kunne optage energi direkte fra solen. Men nu viser det sig, at den orientalske hveps vha. specialiserede celler i sit ydre skellet kan danne elektricitet.De gule dele af hvepsens skelet indeholder pigmentet xanthopterin. Forskere isolerede pigmentet fra hvepsen og brugte det i en normal solcelle-elektrode. Når elektroden blev udsat for kraftigt lys, blev energien overført til pigment- opløsningen, som efterfølgende skabte elektrisk energi. Hvepsens solceller udnytter dog kun solenergien 0,335 pct. effektivt, og derfor må dyret supplere solstrålerne med fast føde. LUFTAKROBATIK guldsmede 🔝Insekter luftakrobatHele 60 procent af den voksne guldsmeds krop består af flyvemuskler. Helikoptervinger styres enkeltvist Guldsmedens vinger er så enestående, at det amerikanske militær og rumfartsorganisationen NASA har forsøgt at udvikle droner med lignende egenskaber. Vingerne er nemlig på én gang lette og stive og alligevel fleksible. Dertil kommer, at guldsmeden kan bevæge de fire vinger uafhængigt af hinanden og på den måde lynhurtigt skifte retning. Ved almindelig flyvning slår vingerne en smule ude af takt, sådan at forvingerne skaber en hvirvelvind, som bagvingerne udnytter til at skabe yderligere opdrift. Folder og blodårer giver ekstrem manøvredygtighed Takket være sine specielle vinger kan guldsmeden vende 180 grader på et splitsekund, Den kan også stå stille i luften, lidt ligesom en helikopter eller en kolibri. Husfluen 🔝Hvor hurtigt flyver en spyflue 🔝Hvor hurtigt flyver en spyflueHar lige set på en, der fløj rundt i stuen. Spyfluer er ret langsomme - ca. 2 m/s, hvilket svarer til ca. 8 km/t, så fart er ikke deres hellige våben. Det er derimod luftakrobatik, da de har gode reflekser. Det samme gælder for stuefluen, som også ligger på en hastighed omkring 7-8 km/t. De hurtigere fluer som f.eks. svirrefluer kan nok flyve omkring 20 km/t. Man kan sammenligne fluen med et 'stunt-propelfly', der ikke flyver så hurtigt, men til gengæld udøver flot luftakrobatik. Skal man op i det, der svarer til et jagerfly, så er det guldsmede, vi skal se på. De kan flyve 50 km/t og intet stopper dem. Forestil dig en formel 1-bil, der ikke behøver bremse i svinget! Guldsmede bruger derfor i højere grad farten som våben, tilsat et fantastisk syn og ligeledes god luftakrobatik. De kan det hele! Hvorfor kan man ikke klaske en flue med hånden, men godt med fluesmækkeren 🔝At det er sværere for fluer, og insekter som helhed, at undvige en fluesmækker end en hånd, skyldes nok en blanding af tyngdepunkt og lille overfladeareal, men også, at der jo er huller i en fluesmækker.Hullerne kan betyde, at der ikke skabes den samme 'luftbølge', som skubbes mod fluen af f.eks. en hånd. Fluen har små hår på kroppen, der hjælper den med at føle ændringer i omgivelserne. Det er heller i ligyldigt hvordan man vender fluesmækkeren, nogle (de billige) er helt flade på den ene side og mere strømlinede på den anden 😀 Den strømlinede side skal ramme fluen ! En tredie mulighed er (igen) hastighed. Fluesmækkeren kommer farende gennem luften langt hurtigere end man kan svinge en hånd. Fluen har dermed et langt kortere undslippelses tidsrum til rådighed. Fluer på PC skærmen 🔝Sidder der en flue på pc-skærmen, reagerer den overhovedet ikke på cursoren (musemarkøren). Den kan ikke skræmmes bort ved hjælp af cursoren. Kan dens øjne ikke opfatte et 'billede' fra skærmen, eller hvad er forklaringen?Der kan være flere årsager til at en flue ikke skræmmes af musen på skærmen: Hvis man kigger på en skærm gennem kameraet på sin telefon, kan man ofte opleve, at skærmen flimrer. Det er fordi, frekvensen på kameraet (FPS/billeder per sekund) og LED-lyset ikke er ens. Det samme gør sig gældende i stopmotion-teknikken, hvor man afspiller en række billeder hurtigt efter hinanden for så at opleve en levende film. Hastigheden, hvorved man oplever, at billederne bliver til levende film, varierer mellem forskellige dyr. Mennesker skal bruge mindst 24 FPS for at kunne nyde en film. En flue skal sandsynligvis bruge en meget højere frekvens. Fluen har altså supergode reflekser - det svarer lidt til, at man kunne se verden i slowmotion og derfor nå at reagere hurtigere. Så det er altså muligt, at fluen slet ikke ser skærmen på samme måde som os. For det andet har fluer et anderledes syn end os og måske svært ved at se musen på skærmen. Fluer har andre sanser end synet, der kan kræve, at der også skal komme stimuli/sanseindtryk fra f.eks. luften. For det tredje: Hvis man tænker over, hvordan fluer oftest bliver angrebet, så er det fra oven eller fra siden. Kun fluer på vandoverfladen skal bekymre sig om angreb nedefra. Det kan altså være, at fluen ikke sanser cursoren, når den bevæger sig under den. Frømøllet - Køkkenmøllet 🔝Når man finder møl i køkkenet, er det sandsynligvis tofarvede frømøl eller alm. frømøl:
Oftest opdager du møllene, fordi du finder fine små klæbrige spind i havregrynene eller melet. Madvarerne kan se klumpede ud, blive gråbrune og/eller lugte. De typiske møl der går i dine fødevarer hedder frømøl (eller myslimøl). Af fødevarer de typisk går i er det; mysli, havregryn, ris, mel, nødder og linser. Mange tror fejlagtigt at det er de flyvende møl i køkkenet, som gør skaden. Det er ikke korrekt, det er derimod møllarverne som spiser og gnaver sig ind til dine madvarer. Frømøl, myslimøl 🔝Fakta om tofarvet frømøl:Larven er gulhvid med mørkebrunt hoved. Størrelse: Larven er 12-13 mm lang, når den er fuldt udviklet. Det voksne møl er knap en centimeter langt. Føde: Møllet lever fortrinsvis af tørret frugt, nødder og mandler, men mel, gryn, fuglefrø, mysli og lignende er også oplagte muligheder. Frømøllets historie 🔝Frømøl stammer oprindeligt fra Asien og blev udbredt til andre verdensdele (inklusiv Europa) i 1840'erne. I dag findes frømøl over hele jordkloden, dog med undtagelse af de meget kolde arktiske egne.Tofarvet frømøl som er den hyppigste møl i danske køkkener, stammer nu om dage fra Sydamerika, hvorfra den med stor sandsynlighed kommer til Danmark ifm. transport af korn eller frugt. I Danmark bliver møllet mere og mere udbredt, det skyldes en øget import og efterspørgsel efter bananer, kaffe, korn, te og andre fødevarer, som ikke dyrkes naturligt på vores breddegrader. Før i tiden var problemet med frømøl og andre tøjmøl meget større end det er i dag. Dette skyldes især, at tøjindustrien i dag anvender langt flere kunstige tekstiler end tidligere. Hertil kommer, at vores viden omkring forebyggelse og bekæmpelse af frømøl i dag er væsentligt mere omfattende og at problemet derfor er nemmere at håndtere nu. Er der brunlige insekter i dit hjem 🔝Er der et fint, klistret spind i dine havregryn, og flakser der små brunlige insekter på størrelse med stuefluer rundt i dit køkken? Så har du sandsynligvis fået møl. Møllene er meget forskellige fra fluer. Møllene er forholdsvist nemmere at tage med en fluesmækker end de almindelige fluer, der er langt mere manøvredygtige og flyver landt hurtigere end møllene.Møl i køkkenet er ofte det tofarvede frømøl (Plodia interpunctella). Det er et meget almindeligt skadedyr i vores køkkener, og det lever af bl.a. nødder, gryn, mel, pasta, mandler og tørret frugt som rosiner. Det kan også være melmøl, men de optræder dog mest i bagerier og virksomheder, hvor mel og andre produkter fra møller opbevares. Man ser flest møl i sensommeren, men du kan støde på dem hele året. Møllets liv og udvikling 🔝Det er umuligt at vide, om møllet har sneget sig med indenfor, når du kommer hjem fra en indkøbstur. For ægget er ikke større end et enkelt sukkerkorn, og det er sådan, invasionen starter. Det lille mølæg kan enten sidde inde i fødevaren eller i emballagens sprækker. Herefter bliver de til nyklækkede larver, der er gulhvide med et mørkebrunt hoved og mellem syv og 13 mm lang.Larverne kravler op ad vægge og i loftet, hvor de gemmer sig i sprækker og hulrum. Efter et par uger forvandler de sig til flyvende møl, der er cirka en centimeter store, lysegrå på den forreste tredjedel og kobberrød med mørke plamager på den bagerste del. Udviklingen fra æg til fuldvoksen tager kun 25 dage, og hunmøl kan lægge op mod 400 æg ad gangen. Hvis møl ikke bliver behandlet, kan der forekomme op til fire mølgenerationer på et enkelt år. Livscyklussens trin 🔝Møls livscyklus kan opdeles i 4 trin:1. Voksent møl Parring: De voksne møl parrer sig umiddelbart efter, at de er frembrudt af deres pupper (parringstidspunktet varierer fra art til art, men finder ofte sted inden for de første par dage efter klækningen – og senest inden for de første par uger). De voksne møls samlede livstid kan være alt fra et par dage til lidt over en måned. Det voksne dyr opholder sig ved foderet døgnet rundt. Det voksne insekt gør ingen skade, men møllarverne fra enkelte arter kan være rigtig træls at få inden for døren. Problemet opstår først, hvis møllet lægger æg, og der kommer larver i klædeskabet eller køkkenet. Æglægning: De voksne møl lægger deres æg direkte på larvernes fremtidige fødekilde. For tøjmøls vedkommende er dette organiske tekstiler (f.eks. i et tøjskab) og for fødevaremøls vedkommende er det tørre fødevarer (f.eks. i et køkkenskab). Nogle arter kan dog også lægge deres æg på plantematerialer eller animalske materialer. Hvor mange æg der lægges, afhænger af møllets art og kan være mellem 40 og 600 i møllets livstid. 2. Æg Klækningstidspunkt: Hvornår æggene udklækkes afhænger i høj grad af temperaturerne og fugtigheden i omgivelserne (og møllets art), men under de rette forhold sker udklækningen typisk efter 4 – 30 dage. Det kan dog tage adskillige måneder. Æggene lægges enkeltvis eller i små klynger på, eller nær foderet og klækker fra få dage og op til 2 uger senere, afhængig af omstændighederne. Selve klækningen: Når ægget klækkes, frembryder møllarven, som straks begynder at æde af den nærmeste fødekilde – hvilket normalt er det materiale, den udklækkes på. 3. Larve Føde: Larvestadiet starter idet larven udklækkes, hvor den som nævnt begynder at æde af sine omgivelser. Hvis ikke larven befinder sig på et materiale, som den kan ernære sig af, vil den straks opsøge et egnet materiale. Tøjmøl f.eks. kan gnave sig igennem syntetiske tekstiler for at få adgang til organiske tekstiler (som de kan leve af), ligesom fødevaremøl f.eks. kan kravle ind ad meget små huller i emballage for at få adgang til fødevaren deri. Næring: Møllarven har brug for en masse næring for at den kan udvikle sig til et voksent møl i det næste stadie; puppestadiet. Under larvestadiet skifter larven sin ham 5 – 45 gange. Larver der er udklækkede på steder med tilstrækkelig føde, bevæger sig næsten ikke omkring. Larver som derimod mangler føde, vil opsøge den så aktivt som muligt og vil derfor vandre omkring. Larvestadiets samlede varighed varierer meget og afhænger især af temperaturer og fugtighed, men også mølarten. Larvestadiet kan vare fra 35 dage til 2 ½ år. Larven æder al slags korn, tørstoffer (majs, tørret frugt, nødder, rosiner m.v.) og måske også tørrede insekter. Udviklingen tager fra 2 uger til 2 år. Larven danner spind og ekskrementer i det inficerede foder. Når den er fuldvoksen vandrer den, til den finder en revne at forpuppe sig i. 4. Puppe Puppen: Larven spinder en puppe (kokon), som den forpupper sig i. Formålet med dette er, at beskytte larven mod udtørring og andre forstyrrelser fra omgivelserne, mens den udvikler sig til et voksent møl. Puppestadiet starter, når larven forpupper sig og slutter når de voksne møl frembryder af sin puppe. Ligesom de øvrige stadier afhænger puppestadiets varighed af omgivelserne og møllets art. Puppehvilen varer 4-30 dage. Der er normalt 6 hudskifter, men under gunstige temperaturforhold kan antallet reduceret til 5 og under ugunstige forlænges til 7. Adfærd: De forskellige mølarter har forskellig adfærd i puppestadiet. Pelsmøl f.eks. vandrer omkring og slæber deres puppe med sig, hvor andre møl har fastspundet deres pupper på deres fødekilder og ikke bevæger sig omkring. Møl eller deres larver – hvem er værst Som oftest finder vi ud af, at vi har fået møl, fordi vi ser de små flyvere flakse rundt i vores hjem. Selve møllene er dog ikke det store problem. Voksne møl spiser rent faktisk ikke noget, så det er ikke dem, der forvolder alle hullerne. Det gør deres larver derimod. Det betyder dog ikke, at vi bare skal lade de voksne møl være, for de lægger jo de æg, som udklækkes og bliver til skrupsultne larver. Derfor er det en god idé at klapse de voksne møl, når du ser dem, og få slået både æg og larver ihjel. Generationer Der kan forekomme mellem 1 og 9 generationer pr. år. Antallet af generationer afhænger i høj grad af møllenes art samt temperaturer og fugtighed i omgivelserne. De optimale temperaturer ligger mellem 20 og 30 grader for de enkelte arter. Alle møl, larver og æg dør hvis de opvarmes til 60 grader i en time. De kan godt overleve frost, men langt de fleste dør ved -18 grader (i mindst 2 døgn). De er desuden meget følsomme overfor store temperaturudsving, og vekslende kulde og varme tager derfor livet af dem. Fugtigheden er især vigtig for frømøllene, hvis udvikling bremses eller ophører, hvis ikke der er tilstrækkelig fugt i omgivelserne. Det invasive skadedyr møl er vokset hastigt frem i hele landet det seneste årti. Og bestanden bliver kun større for hvert år, advarer skadedyrseksperterne. Hold øje med:-Møl der flyver rundt i køkkenet eller andre steder i boligen, hvor de typisk er aktive i aftentimerne.-Om der er spind, larver eller voksne møl i kolonialvarer såsom frø, nødder, mel, ris, mysli eller lignende. -Om gulhvide larver sidder i loftet, i sprækker, ved loftslister eller øverst i skabe. Møl er ikke farlige eller giftige! 🔝Larverne og møllene er ikke giftige eller på anden måde farlige, og vi har nok alle spist en larve eller to. De siges at være meget proteinrige.Men det er derimod skadeligt at indtage møllets eskrementer i større mængder. Sådan undgår du møl i madvarerne 🔝
Økologi, giftfri madvarer vs. frømøl 🔝Frømøl er ofte et problem i forbindelse med økologiske tørvarer som nødder, gryn, mel og mandler. Dette skyldes, at varerne ikke er udsat for den samme forebyggende møl bekæmpelse som de ikke-økologiske varianter.Frømøl spredes ofte via producenter og detailhandel til forbrugerne. Dyrehandlere er for eksempel hårdt plaget af tofarvet frømøl, da tørfoder er en primær kilde til møl. Også melproducenter bidrager til forekomsten af møl i private hjem, især i forbindelse med økologiske tørvarer. Frømøl i køkkenet kan dog i mange tilfælde være selvforskyldt, hvis der ikke holdes en høj køkkenhygiejne, og tørvarer ofte får lov til at stå for længe. Økologiske tørvarer er også en hyppig kilde til både frømøl og melmøl i køkkenet. Det er derfor vigtigt at holde køkkenet rent og fri for gamle tørvarer for at forebygge angreb fra frømøl. Økologiske produkter, der ikke er beskyttet med konserveringsmidler, kan være særligt udsatte for frømøl. For at undgå frømøl kan man opbevare tørvarer i tætsluttende beholdere og regelmæssigt tjekke for tegn på mølangreb. Melmøl, hold dit hjem frit for dem 🔝Melmøl er grå sommerfugle, og de bliver tit forvekslet med tofarvede frømøl. Melmøl og frømøl er mindre udbredte end eksempelvis pelsmøl og klædemøl, der lægger sine æg i dine møbler og klædeskabe.Melmøl er en type møl, der går i dine fødevarer. Her lægger de deres æg, og når larverne bliver klækket, spiser de af din mad. Dette gør din mad uspiselig for mennesker, og dermed forvolder de altså stor skade på dine fødevarer. Men selvom de ikke er meget udbredte i Danmark, så lever de her. Og det er ikke sjovt at få melmøl og deres afkom i sine skuffer og skabe med mad. Derfor er det vigtigt, at du forebygger, så melmøl og andre skadedyr får så dårlige betingelser for at indtage din mad som muligt. Men er skaden sket, kan du heldigvis selv komme problemet til livs. Du får svar på, hvordan du forebygger samt slipper af med melmøl herunder. Sådan forebygger du angreb fra melmøl 🔝Det vigtigste du kan gøre for at undgå, at der kommer melmøl i din mad, er, at du opbevarer det godt og sikkert. Du skal bruge tætlukkede beholdere, for her kan melmøl ikke komme igennem. Larver fra melmøl kan godt kravle gennem små åbninger i de pap- og papiremballager, som eksempelvis mel og havregryn kommer i. Men hælder du det i en forseglet beholder, kan de ikke.Hvis skaden er sket 🔝Hvis skaden allerede er sket, findes der et middel, en fælde, fra firmaet "Green Protect", som er ret effektiv. Firmaet har forskellige mølprodukter herunder et, der er specielt rettet mod "Mel og Frømøl". De har et tilsvarende middel mod klædemøl o.a., det er rart at vide.Mølfælderne virker ved at de udsender Feromon dufte, som mennesker ikke bemærker, men som tiltrækker især han-møllene. Når møllene lander i fælden klistres de uhjælpeligt fast og dør ret hurtigt. Mølfælden der er specielt rettet mod hanmøl, fanger ikke andre insekter i udbredt grad, og hver fælde er aktiv i op til 6 uger. Fælderne forhandles fra helsekostforretninger og planteskoler og kan desforuden forskrives via internettet 😀 Google feks: "green protect mølfælde". Typisk pris: Kr. 60,- (+ evt fragt) for 2 fælder. Og den virker ! Men husk at fjerne epicenteret for udklækningen 😀 [Denne side har ingen forbindelser til "Green Protect", hverken økonomisk eller andet samarbejde og kan følgeligt ikke holdes ansvarlig for brug/misbrug af firmaets produkter.] Elektriske Mølfælder 🔝Er du træt af irriterende insekter i dit hjem? Den elektriske insektfanger med UV-A lys er den ideelle løsning til at holde dit hjem fri for fluer, myg og andre insekter. Den effektive insektdræber tiltrækker og eliminerer insekter hurtigt og sikkert.Mange insekter, herunder fluer, møl og myg, er tiltrukket af UV-lys, fordi det efterligner lyset fra solen og blomster, som de navigerer efter. Dette fænomen udnyttes i elektriske insektfanger-enheder, der bruger UV-A lys til at tiltrække og dræbe insekter effektivt. Forskning og praksis har vist, at UV-lys er en effektiv metode til insektkontrol, især i lukkede rum og nær lyskilder, hvor insekter naturligt flokkes. UV-A lyset tiltrækker insekter, som derefter elimineres ved kontakt. Designet er sikkert for børn og kæledyr, og det anvender ingen kemiske bekæmpelsesmidler, hvilket gør det til et sundt valg for dit hjem. Tilslutningen er meget simpel: du skal blot sætte den i stikkontakten og tænde den. Den elektriske fluefanger dækker rum op til cirka 20 m² og har et ekstremt lavt energiforbrug, hvilket gør den både effektiv og økonomisk. Cedertræ imod møl 🔝
Skægkræ 🔝Sølvkræ - Sølvfisk 🔝Ildtæge - Kastaniemøl 🔝Ildtæge 🔝Kig efter den røde ildtæge derude. Den er blevet mere udbredt i de senere år. Ildtægen lever af plantesaft.Mildere klima har fået ildtægen til at brede sig mod nord. Ildtægen er en tæge som navnet fortæller og den har altså intet med en flåt at gøre. Det til trods for, at mange stadig forveksler flåter og tæger. Ildtægen er relativ ny her i landet, selvom det er omkring 100 år siden, at man fandt de første eksemplarer herhjemme. I landene syd for os er den udbredt, men Danmark ligger stadigvæk i den nordligste del af dens udbredelsesområde. Flere fund de seneste år og ikke kun i Syd- og Sydøstdanmark tyder dog på, at med det mildere klima føler ildtægen sig også hjemme i Danmark. Det betyder, at den ikke er så sjælden mere. Faktisk blev den første ildtæge fundet i Norge i 2020. Hvordan de spreder sig, er dog stadigvæk lidt af en gåde, da størstedelen af ildtægerne ikke kan flyve. Kastaniemøl 🔝Træer af hestekastanie med efterårsfarver sidst i juli, kan skyldes angreb af Kastanie-minérmøllet (Cameraria ohridella).Kastanie-minérmøl Nye skadedyr og svampesygdomme indfinder sig fra tid til anden i Danmark. Måske et resultat af den stadig større kontakt og samhandel med vore nabolande. Det drejer sig her om et lille møl som tidligere især var kendt i centraleuropa, men som siden 2002/2003 har bredt sig til det meste af landet, dog først og fremmest Sjælland og Øerne. Den voksne møl lægger æg på katanieblade. Æggene klækkes til minérende larver, som lever inde i bladene. Insekters indre anatomi 🔝Se også skitsen af fluen i venstre spalte !Tarmkanalen 🔝Tarmkanalens forreste afsnit bærer på indersiden en kutikula, der hos mange højere insekter har en karakteristisk tandbevæbning eller udvides til et fødereservoir. Så følger en midttarm, som er hovedsædet for nedbrydning af føden og optagelse af næringsstofferne. I grænseområdet mellem mellem- og bagtarmen indmunder de malpighiske rør, som er de vigtigste ekskretionsorganer. Bagtarmens inderside er som fortarmens klædt med en kutikula; dette tarmafsnit rummer celler, der er specialiseret til vand- og iontransport, og som sammen med de malpighiske rør regulerer blodets saltbalance.Nervesystemet 🔝Insekternes nervesystemNervesystemet består af og en bugnervesnor (abdominal gangliekæde), der strækker sig igennem hele insektet, og er forsynet med en nerveknude (ganglion; flertal: ganglie) for hvert segment. Det første ganglion, som ligger foran mundåbningen, er specielt stort og omtales som hjernen. Den abdominale ganglionkæde ligger i bugsiden og afgiver nerver til kroppens muskler og sanseorganer. De første to af dets ganglier, det øvre og det nedre svælgganglion, befinder sig ligesom hjernen i hovedet og er begge forbundet med en kort nervesnor (kommissur) på hver sin side af munden. Den abdominale ganglionkæde består af et antal (op til 11) med dobbelte nervesnore forenede nerveknuder. Af disse er dog i fuldt dannede insekter flere sammensmeltede med hinanden, og hos nogle arter er de endog forenet til en enkelt masse af ganglier placeret i mellemkroppen, for eksempel hos fluerne. Udover dette nervesystem har insekterne et andet nervesystem, det såkaldte sympatiske nervesystem, som består af mindre, parrede eller uparrede ganglier, forbundet med langsgående nervesnore, der står i forbindelse med dels det øvre svælgganglion, dels med den abdominale ganglionkæde. Hjernen er forbundet med kirtler, der producerer hormoner, som regulerer hudskifte, kønsmodning m.m. På kroppens overflade findes sanseorganer, som registrerer mekaniske og kemiske stimuli. En særlig type mekaniske sanseorganer, chordotonalorganerne, findes kun hos insekter og krebsdyr. De er placeret ved de fleste led, og mærker leddenes bevægelser i forhold til hinanden. Reproduktion 🔝Insekter lægger mange æg, hvilket hænger sammen med, at de er langt nede i fødekæden. Mange unger bliver spist, hvorfor arten er nødt til at reproducere sig selv mange gange for at overleve.Insekters respiration og cirkulationssystem 🔝Insekter har ikke lunger eller andre former for aktiv respiration. I stedet tillader de luften at passere passivt ind og ud gennem åbninger på kroppen. Der er forskellige åndedrætssystemer blandt insekter. Den ene hedder trachésystemet (#8 på flueskitsen i v. spalte) og består af rørformede passager, der er fyldt med luft. Et andet system, der ofte ses hos spindlere som fx skorpioner og edderkopper, kaldes boglunger. Disse består af hule blodfyldte lameller, der ligger parallelt, ligesom siderne i en bog. Mellem disse lameller er der luft, så der kan ske gasudveksling mellem luften og blodet. De fleste insekter har muskler, der kan lukke åndehullerne for at reducere lufttilstrømningen. Nogle insekter kan forlænge bagkroppen og derved øge luftstrømmen i kroppen. Hos nogle akvatiske insektlarver mangler der åndehuller, og i dette tilfælde er der ofte bladlignende eller trådlignende såkaldte luftrørsgæller på siderne af bagkroppen, hvorigennem den ilt, der er opløst i vandet, kan absorberes ved diffusion.Nært knyttet til åndedrætsorganerne er et insektspecifikt organ, det såkaldte fedtlegeme. Det består af en mængde ophobede fedtceller, mellem hvilke ekstremt talrige og fine luftrørsgrene trænger ind. Fedtlegemet fungerer hovedsageligt som et energidepot. Eftersom åndedrætsorganerne er fordelt over hele kroppen er det ikke nødvendigt at have et avanceret blodomløb. Blodkredsløbet består kun af et enkelt, opdelt pulserende kar, der løber langs ryggen og er delt op i kamre af muskelbundter, som driver den farveløse blodvæske fremad, til nærheden af hovedet. Der mødes blodkarrene, og blodet spreder sig frit i mellemrummene mellem kroppens organer. |
|